
Есть у меня недостаток: не могу задушить в себе критика. Если я с чем-то категорически не согласна, то меня аж потрясывает от потребности возмутиться. Казалось бы, дыши ровно, иди мимо, так нет ведь… На сей раз всплеск активности спровоцировал пост о развитии детей одной женщины. Если бы просто мама, я бы не встревала, но она автор интернет-проекта, а значит, транслирует своё мнение многим родителям. Поэтому, для равновесия точек зрения, я транслирую своё.
Сам пост: «Если малыш где-то услышал слово «депозит» и хочет узнать его значение, не надо мучать его процентами и сложными вычислениями. Ведь можно же объяснить смысл этого слова. Например, так. Чтобы в магазине взять еду, нам нужно в обмен за товар отдать денежку. А где ее взять? Способов очень и очень много. Один из них — это хитрый депозит. Нужно взять несколько денежек и отнести их в банк. Тетя заберет у тебя 5 денежек, а через год вернет 7 денежек. Вот и станет у тебя на 2 денежки больше. Пока ты занимался своими делами, твои денежки росли и размножались. Ведь можно же так объяснить ребенку? И не важно, что в цифрах приведены нереальные проценты. Не важно, что не описан процесс того, откуда берутся у тети эти 2 дополнительные денежки. Не важно заморачиваться на том, что купюры могут быть разных номиналов»
Не важно?!! Очень даже важно! Важно соблюсти процентное соотношение как правило реалистичности модели. Важно затронуть тему, каким образом тётя «выращивает» деньги. Ребенку для понимания нужна реалистичная целостная модель с установленными взаимосвязами. Лучше так: «Отдаешь тёте на хранение 10 монет. А Вася, наоборот, берет у тети 10 монет. Через год Вася отдает тёте 12 монет, потому что они так договорились. Из них тётя, отдает тебе 11» Если объяснять, то сразу в системе. Иначе создается ложное представление, что можно отнести пять монет и добрая тётя просто так накинет две сверху. Другой бы ребенок в этом случае спросил, почему тётя не может просто так дать две монеты? Почему только две, а не десять? И зачем, мама, ты вообще ходишь на работу, если есть добрые тети с хитрыми депозитами. (При нашем уровне инфляции воспринимать депозит как способ размножения денег? Ну, извините…) Если малыш способен понять про депозит, то и про кредит поймет, ибо объяснение абсолютно аналогичное. Зато создается целостная картина.
Но оппонент остается при своем мнении: «Если же для ребенка вычитание и сложение еще представляют сложность, так как он с ними еще не знаком, зачем его загружать и путать лишними элементами за один раз? Предложенный мной вариант воспринимается ложным, если его так и оставить без дальнейших объяснений. Откуда тетя взяла деньги, и почему через год деньги потеряли ценность? Но если разбить целостное объяснение на несколько этапов, то потом картинка из пазлов сложится воедино»
Это дидактическая ошибка. Нельзя формировать хоть временное, но ложное представление. Это все равно, что показать картинку с хоботом слона и дать название «хобот», а с остальными частями тела познакомить через год. Ведь ничего страшного, что некоторое время ребенок будет думать, что хобот — это животное, похожее на удава. Потом все поймет, когда получит остальные элементы пазла. При таком подходе у ребенка не формируется системность мышления. Образно говоря, у человека, привыкшего получать знания в таком разрозненном виде, без установления взаимосвязей, не будет потребности в выстраивании целостной картины, он не будет фанатично искать недостающие элементы системы (пазла) и задавать проясняющие вопросы. Можно ведь просто прихватить яркий кусочек от чего-нибудь, авось пригодится… И будет такой человек носить с собой набор элементов от разных пазлов в мешочке, периодически что-то изымать и с гордостью демонстрировать. При этом пребывать в иллюзии, что он много всего знает. Системность — важный дидактический принцип, суть которого хорошо отражена в философском тезисе: «Целое больше суммы своих частей»
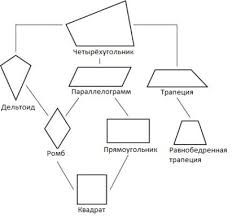
Для развития лучше давать меньше знаний, но в системе, формируя таким образом привычку структурировать поступающую информацию, искать и устанавливать связи между отдельными элементами. Очень тяжело переучивать детей, которые выучили, что есть квадрат, прямоугольник, ромб, трапеция, параллелограмм, но все вне системы. Они спорят, что вот это квадрат, а это прямоугольник. И не понимают, что квадрат – это тоже прямоугольник. А еще квадрат — частный случай параллелограмма. И ромбом квадрат тоже является. Это даже в седьмом классе некоторые с трудом понимают. Увы, системное мышление само собой не формируется.
Грустный факт, но у нас действительно много людей неспособных мыслить системно. Пример несистемного мышления взрослого человека: «Сколько живу, никак не могу понять, почему государство не напечатает столько денег, сколько нужно» Еще грустней, когда люди, не обладающие системным мышлением, добираются до руководящих постов. Тем страшней последствия их ошибок. Ошибок, которые являются следствием фрагментарного мышления – узкого, без учета сопутствующих факторов, без понимания причинно-следственных связей.
Человеку с системным мышлением невозможно что-то впарить. Он не верит яркой фрагментарной информации, ему для принятия решения необходимо выстроить целостную систему. А если система не выстраивается, значит, в чем-то подвох.
— У нас используются только натуральные ингредиенты в косметике!
— А что же тогда вы используете в качестве консервантов?
— Мы их не используем!
— Вы понимаете, что без консервантов она не сможет храниться? А состав вы сами читали?
Или так:
— Наш пылесос позволит экономить до 20000 рублей в год за счет снижения потребления энергии!
— Вам эту сумму сказали на тренинге продаж? А Вы ее проверяли? Вы сами сколько платите за электроэнергию в месяц? Вы понимаете, что 20000 в год я не сэкономлю даже если совсем перестану пользоваться электроэнергией.
При фрагментарном подходе мы выдаем информацию по мелким кусочкам. Совсем не факт, что ребенок захочет потом сопоставить их и найти недостающие. При системном подходе мы показываем целостную картину, а впоследствии дробим на все более мелкие детали, углубляясь в подробности, которые со временем становятся доступными для понимания.
При фрагментарном подходе ребенок может знать, что он вырос в животе у мамы из маленькой клеточки, и при этом верить, что его приятеля нашли в капусте, а подружку купили в магазине. При системном подходе ребенок знает, что он — часть природы, часть животного мира, что процессы размножения схожи у разных животных. Что абсолютно каждый ребенок вырастает из клеточки.
При фрагментарном подходе ребенок считает, что волк плохой, потому что съедает хорошего зайчика. При системном подходе ребенок понимает, что волк и зайчик — звенья пищевой цепочки.
При фрагментарном подходе ребенок заучивает домашний адрес «Улица Пушкина» и спорит, что он живет на Пушкина, а не в Екатеринбурге. При системном подходе ребенок знает, что улица находится в Екатеринбурге, а Екатеринбург – город в России. Он легко встроит в эту систему любой город мира по критерию «находится в России или нет» Теория множеств для дошкольников? Легко!
При фрагментарном подходе ребенок зубрит таблицу сложения как странный стих без рифмы. При системном — он понимает общий принцип и сам доходит до операции умножения, радостно сообщая однажды: «Сто раз по сто — это десять тысяч!» В пять лет реально даже начинать знакомить с понятием возведения в степень. Меня умиляет, когда Сашка говорит не «дофига раз», а «додекальон раз» (Я сама чаще говорю «дофига») А я в его годы никак не могла понять, почему не существует самого большого числа…
При фрагментарном подходе ребенок запоминает картинки и названия: треугольник, квадрат, прямоугольник. И не задумывается, что бывают другие фигуры. При системном подходе ребенок понимает, что это все – фигуры. Что треугольник – это потому что три угла, а если угла четыре, то это четырехугольник. Что четырехугольники бывают разные. А если у фигуры пять углов? Пятиугольник! И можно уже картинку не показывать — ребенок сам нарисует по аналогии. А круг – это правильный бесконечноугольник. Потому что правильный N-угольник при увеличении параметра N все больше похож на круг – проверяется экпериментально в графическом редакторе. Элементы математического анализа в дошкольном возрасте? Легко!
Сегодня Сашка (напомню, что ему пять лет) поделился своим открытием: «Четное плюс четное всегда будет четное число!» Я спросила: «А ноль — четное или нечетное» Задумался. «Четное! Конечно четное! Оно же между нечетными числами стоит: один и минус один!» Ребенок, уловивший общий принцип, сам находит ответ на вопрос.
Системное мышление в дошкольном возрасте — это умение соотносить часть и целое, причину и следствие, искать общие признаки и принципы, искать отличия, уметь обобщать. Учите детей устанавливать взаимосвязи между фактами, процессами и явлениями.
Анна Быкова






Всем мамам бы да техническое образование 🙂
Образование может быть любым. У меня просто примеры из области математики, так как сама учитель математики по первому образованию.
Тогда еще пример, бытовой:
Соседская девочка Кристина сообщает мне о планах на вечер:
— Мы сегодня с мамой пойдем на День рождения. Я только не очень помню к кому. То есть я знаю, к кому мы пойдем, но будет ли День рождения тети или дяди, или брата — я не помню. Но торт будет обязательно!
Я с пониманием киваю. Торт — это очень важно. А Кристина восторженно продолжает вещать.
— У меня так смешно: День рождения всегда весной. У других бывает летом, зимой, осенью. А у меня всегда весной. Каждый год весной получается и ни разу даже осенью!
В восприятии Кристины День рождения — это просто праздник конкретного человека, не привязанный к определенной дате и конкретному факту появления на свет. Как-то этот момент ей объяснить забыли. Так бывает, взрослые скажут что-то с высоты своего опыта и своих знаний в полной уверенности, что ребенок их понял нужным образом. А у ребенка в голове совсем другая картина выстраивается. Вот, например, у Кристины относительно Дня рождения получился некий генератор случайных чисел…
Здравствуйте! Прочитала вашу статью, причем несколько раз, и почувствовала себя немного обделенной девочкой . Вы настолько правы , что я даже теряюсь.. В наше время обучения не учили системному мышлению )) у меня ребенку 9,5 месяцев , а ведь до его вопросов осталось совсем немного .. И наверное для начала нужно научится этому , а потом объяснять ребенку . Как это сделать ? У меня самой два высших образования , причем техническое и гуманитарное ))) я благодарна, что есть такие специалисты, как вы, которые переворачиваюсь мышление с ног на голову у родителей !
Анна, добрый день! спасибо за статью, но мне думается, что не все можно объяснить с позиций системного мышления ребенку любого возраста… Мой пример: в шестом классе по географии дети проходят тему «Горы». И им объясняют, что Урал — так называемые старые горы, а вот Кавказ — горы молодые. Только в восьмом классе, когда дети постарше, им говорят, что не горы, а земная кора в горах разного возраста: на Урале — более древняя, а на Кавказе — более молодая, а все горы на Земле образовались одномоментно, несколько миллионов лет назад. То есть, только спустя 2 года информацию в их голове дополняют, потому что эта теория — образования земной коры и рельефа — действительно очень сложна для понимания. После 5 лет обучения на географическом факультете для меня разница в возрасте земной коры на разных участках Земли очевидна, но как ее, эту разницу, объяснить шестиклассникам?..
Спасибо. Замечательная статья. Я тоже учитель математики и понимаю важность системного подхода. Проблема только в том, что все методики этим не блещут. В системном подходе работают тематические недельки.
Анна! Спасибо, что поделились своим подходом! Я еще не дочитала статью, но про «хобот» это, как про меня написано )))) Меня никто не учил мыслить системно. Важность этого я поняла только в 30, когда сыну годик исполнился. Теперь учусь сама и его учу структурному мышления. А Ваша статья поможет соблюдать важность целостности картины!
Елена, в школьном курсе географии нет противоречия с системным подходом. Целостная картина о разнообразии форм рельефа выстраивается, а «впоследствии дробим на все более мелкие детали, углубляясь в подробности, которые со временем становятся доступными для понимания».
Анна, спасибо! Великолепная статья! Вы правы. Частные случаи маме самой нужно понимать, как объяснить, но обязательно системно. Это очень полезная статья, браво!
Анна, как Вы правы. Я долго размышляла об этом и пришла к выводу, чтобы дать понятное и полное объяснение ребенку какого-то явления (чаще всего, ответить на очередное «почему») да ещё на понятном малышу языке, нам нужно самим в целом представлять то, о чём сейчас будем говорить. Зачастую мы, взрослые, сами плохо представляем весь пазл! Сама столкнулась с этим с трелетней дочкой. Как это ни печально. Чтобы интересно и понятно что-нибудь объяснить или рассказать, во-первых, мама сама должно знать это в подробностях, во-вторых, маме должна нравиться эта область знаний. Например, многим хочется, чтобы ребенок с малолетства говорил на английском. Тогда кто-то из близких родственников должен говорить на этом языке и получать от этого удовольствие. И малыш подхватит и продолжит, если остальные окружающие поддержат это начинание в ребенке. Если же мама в математике, или истории, или географии или в друугой области знаний — «ноль», то и увлечь ребенка при огромном желании не сможет. А при очередном детском «почему» даст ответ подбно тому, который вызвал у Вас возмущение. В общем, сейчас я по мере своих возможностей интенсивно восполняю пробелы в моих знаниях ))) чтобы не приходилось давать своей доченьке неполных ответов.
А я подумала, что ребёнок, которому так объяснили про депозит, когда вырастет обязательно вляпается в какую-нибудь «МММ»…
Спасибо за статью! нравится читать ваши тексты. Но после этой статьи начала копание в себе и поняла, что стремление к системности и аналитичности у меня есть, это и преподаватели в вузе отмечали. Но в жизни часто включается ленивец, которому не хочется «дойти до самой сути». Впарить мне что-нибудь сложно, тут уж я себя в обиду не дам:-) но в житейских разговорах мне лень при каждом случае выстраивать целостную картинку
С одной стороны, полностью с Вами согласна, Анна. С другой стороны, многие примеры смущают. Ведь именно обилие информации, лишней для конкретного возраста, приводит очень часто к каше в голове, т.е. отсутствию системности. Тому пример ваш комментарий про географию. А часто недостающее звено в подаче информации и стимулирует мышление, заставляет искать ответ, задавать дополнительные вопросы. Обычно это знак, что информация подана вовремя для данного конкретного ребенка. Если взрослому кажется, что ребенок должен задавать вопросы, а он словно все понял и не хочет дальше размышлять, то этому взрослому следует помочь ребенку наводящими вопросами, так и выстраивается система. Многое тут зависит от работы мозга, от его развитости, от способности усваивать ту или иную информацию. Да и очень мало взрослых способных системно, логично и последовательно передавать информацию, и никто точно не знает в каком объеме это делать. Я лично не считаю нужным маленькому ребенку знать про депозиты и кредиты, это лишнее. Ваше объяснение настолько же не понятно, как и объяснение мамы, вас возмутившее))
Наталья, каша в голове скорее всего образуется при фрагментарном подходе, когда идет обилие несвязной информации. Если новая информация связывается с уже имеющейся — а это есть одно из условий реализации принципа системности — то она легче усваивается.
Недостающее звено стимулирует мышление и побуждает искать ответ только в случае, когда ребенок уже привык получать информацию системно, привык устанавливать связи между фактами и явлениями.
Я тоже не считаю нужным объяснять ребенку про депозиты и кредиты, кроме случаев, когда ребенок САМ интересуется. Именно эта ситуация и разбирается. Если ребенок спросил — не оставлять же его без ответа. Понятно или не понятно — зависит от конкретного ребенка, от уровня его подготовленности и способности взрослого к объяснению. Если ребенок задает вопрос про депозит, то, вероятно,уже способен понять объяснение.
Это не мой подход. Этот дидактический принцип предложен Я.А. Коменским.
«Если новая информация связывается с уже имеющейся — а это есть одно из условий реализации принципа системности — то она легче усваивается.» — Анна, с этим абсолютно согласна. Тогда и получается, что один новый фрагмент накладывается на другой уже ранее знакомый фрагмент, а через некоторое время добавляется еще один фрагмент — и вот уже сложился пазл, картинка, т.е. система. Система без звеньев не существует. Каша получится, если выдавать все составляющие системы сразу. И для маленького ребенка абсолютно нормально путать какие-то вещи, потому что в своем возрасте он не может всего знать, но со временем у него все встанет на свое место. Лишь бы действительно получение знаний было бы последовательным, а это зависит от взрослых. Именно поэтому мне ваша статья очень нравится, она заставляет взрослых задуматься. Просто не покидает ощущение, что при этом в ней есть противоречия.
А слово «депозит» для ребенка — это просто новое незнакомое слово, звучание и вряд ли ребенок, спросив про него, готов все про него выслушать и понять))) У меня есть знакомая, у которой ребенок очень любил слово «подонок». Как бы ему не объясняли, ему было все равно, ему нравилось его особое звучание, необычное, как ему казалось, сочетание звуков. Он его произносил, словно пел и от этого был счастлив)))
пошла искать. спасибо большое!
Анна, спасибо за статью! Полностью с Вами согласна. Но вы меня немного смутили примером про геометрические фигуры. Моему сыну 1 г 3м, я сама занимаюсь с ними по логике тематических неделек (или двухнеделек), выбираем тему и играем, читаем, смотрим, ищем в книжках, на улице и т.п. Сейчас как раз неделя геометрических фигур, сын любит свой сортер с фигурками, вкладыши, липучки в виде кругов и т.п. Но я не пока решила не акцентировать внимание на количестве углов, сторон, даю много фигур потрогать, пощупать (Блоки Дьенеша, аппликация из бархатной бумаги), даю ему возможность самому прийти к тому, чем квадрат отличается от прямоугольника. Неужели это фрагментарный подход?
Ксения, Блоки Дьенеша — замечательное пособие. Акцентировать внимание на количестве углов будете позже, когда малыш освоит количественный счет. Сейчас акцент на сенсорику и моторику — вполне достаточно. Пусть все трогает, пробует. Позднее можно выстраивать связи по следующим критериям: цвет, размер, форма.
— Такая же деталь
— Деталь такого же цвета
— Деталь такой же формы
— Деталь такого же размера
— Такого же цвета, но другой формы
— Такой же формы, но маленькая
и т.п.
Если только ради общего интереса. Почитать историю педагогики.
Анна, спасибо!
ой, а мне муж вот недавно объяснял то же самое (про горы), но не из курса географии он об этом знает, а из детской энциклопедии, которую читал еще до школы! И сколько всего еще рассказывает! И про планеты и космос, явления различные, и физические явления, долго перечислять… При том, что с ним больно то никто не занимался в детстве… И он во многом превосходит в системном мышлении окружающих.
О системности мышлении мне тоже он впервые рассказал. И поделился «печалью», что нам в жизни этого ой как не хватает, и окружающим.
И я понимаю, что училась, не умея учиться, отвращение к учебе — единственное воспоминание о школе, хоть и не троечница совсем даже, и высшее техническое имеется. Приспосабливалась кое-как, чтоб с первого раза все сдать и не вспоминать. И по что нам такое высшее?
Узнали, что в вальдорфской системе развивают системное мышление. Вот надеемся, что сможем присоединиться к ней.
Спасибо за статью.
Чтобы развивать системное мышление необязательно искать специальные методики или школы. Достаточно просто при подаче новой информации соблюдать основные принципы. Как-нибудь расскажу о них. Возможно, сделаю вебинар на эту тему.
Анна, а тебе не показалось, что твое объяснение ничем не отличается от тетиного
«Отдаешь тёте на хранение 10 монет. А Вася, наоборот, берет у тети 10 монет. Через год Вася отдает тёте 12 монет, потому что они так договорились. Из них тётя, отдает тебе 11»
А почему Вася отдает на 2 монеты больше? Тоже просто накинул? Ты переносишь эти 2 монеты чуть дальше. По сути прячешь так же как и то объяснение которое критикуешь.
А в целом я согласна — системное мышление надо развивать. И математика, логика — это только вершина айсберга. Кстати дети 5-6 лет отлично понимают и сами слова система-подситсема-надсистема.
Нет, Ксюша, не показалось. Есть принципиальное отличие. Во-первых, в моем примере выдержано реалистичное процентное соотношение. Во-вторых, в примере сказано, что Вася отдает на 2 монеты больше не просто так, а потому что они с тетей так договорились — взаимовыгодные условия. В-третьих, система выстроена; пусть примитивная, но целостная и реалистичная модель. Сравни с посылом «не важно, что в цифрах приведены нереальные проценты. Не важно, что не описан процесс того, откуда берутся у тети эти 2 дополнительные денежки»
Аня, так и в первом случае: вы договорились, что тетя отдаст на 2 денежки больше. Во всяком случае и вы и тетя знаете это заранее — а это и есть договор.
Аня не поняла насчет реалистичного соотношения. То есть 40% годовых (2 от 5), это не реалистично, а 10% ближе к правде (1 от 10)? Но ведь банки и ситуации существуют разные. И депозит то НЕ ВСЕГДА банковский вклад под 10%.
Депозит это — финансовые инструменты, помещаемые для хранения в кредитные учреждения и подлежащие возврату внесшему их лицу на заранее оговорённых условиях. Ни слова о процентах и банках…
Честно: у тебя система чуть лучше, чем у тети, но сказать, что она формирует четкую и реалистичную модель или даже СИСТЕМУ по-моему нельзя.
Ксюша, спасибо за мнение. А как бы ты объяснила пятилетнему ребенку, о каком депозите ты только что говорила с папой?
Ирина, здравствуйте! Если вы меня «слышите»))) Поделитесь-как?!
«В общем, сейчас я по мере своих возможностей интенсивно восполняю пробелы в моих знаниях ))) чтобы не приходилось давать своей доченьке неполных ответов.»
Какие-то детские энциклопедии?
Ольга, слышу ))) Да, я поплняю свои знания. Начала с детских энциклопедий. Они написаны как раз для взрослых ))) интересно и доступно, ещё и кратко, но основную идею передают. Ну и если есть уточняющие вопросы, то уже в интернете. А вы как?
Ирина, я только почувствовала острую необходимость этого пополнения, поэтому и спрашиваю методы. а какие у вас энциклопедии?
Аня, спасибо за статью!
Скажите пожалуйста. Вот я бессистемный человек. Могу ли я уже в зрелом возврасте стать системным? И какие нибудь простые советы можете дать? Если это возможно стать системным во взрослом возврасте(
Лучше всего системное мышление формирует математика. Судоку и другие математические головоломки.